Bad balls beget bad balls
Using ball-tracking data to investigate a common assumption: are elite bowlers prone to overcompensation?
The internal algorithm of cricket is complex. Under specific conditions, it can be shown to be rational for players to persist with a strategy that had brought them success in a past period or eschew an action that failed them previously because players cannot point out precisely why an action must have produced a particular outcome. This causes them to engage in activities that may be seen from afar as based on primitive rationales such as recency bias, but underlying this perceived impatience is an acknowledgment of the complex forces guiding the sport. Thus, it is not immediately obvious that overcompensation of bad balls is a bad tactic.
To overcompensate is to respond to bowling a full one on the pads by sending down a short and wide one immediately afterward. Both are almost equally bad balls in general, but a combination bowlers may inadvertently go for because they can’t help but overcorrect their lines or lengths after being clipped for a boundary off a poor ball. It is something elite hitters such as Glenn Maxwell are constantly on the lookout for, as several excerpts from his autobiography reveal:
With Shami angling in at his off-stump, Heady had the touch required to steer where deep third had been taken out - a precious four. Per the plan for any batter, an overcorrection followed with Shami getting full, letting our gun opener smash him through mid-on.
- Maxwell regaling the 2023 ODI World Cup final
Can overcorrection of ball types be observed in the data? T20 is the ideal venue for analyzing overcompensation because it is in this format that batters attack the most. Though limited in many ways, ball-tracking data from the last three IPL seasons can be leveraged to see how robust the tendency to overcompensate is. It also lets us settle an important question: are elite bowlers of superhuman capabilities prone to mistakes widely reviled as irrational? Or could it be the case that the extreme complexity of T20 cricket renders acting on limited but recent evidence valuable?
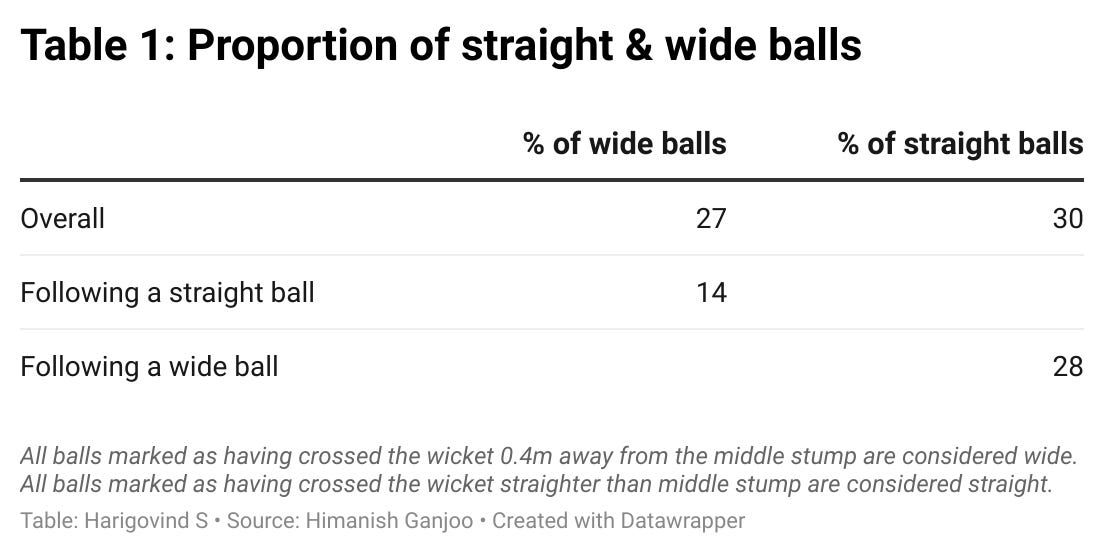
We start by asking the following basic question. Given a ball is straight and on the pads, what is the probability that the ball succeeding it, bowled by the same bowler, will be wide and outside off? Analogously, what is the probability that a wide ball will be followed immediately by a straight one? The results are shown in Table 1. This elementary query will only get us so far, for a few reasons. Firstly, bowlers usually bowl to pre-set plans, so it could be argued that any succeeding ball will likely mimic the features of its predecessor. Secondly, even when there isn’t a general change in lines from one ball to its successor, perhaps it could be the case that certain outcomes force a bowler to overcorrect their lines - such as a boundary for instance. In other words, it is important to account for such heterogeneity.
Our initial question must hence be tweaked a bit. We instead ask two related questions. Firstly, what is the probability that a ball will be of an overcorrected line given that its predecessor was straight or outside off and produced a boundary or a wide? Secondly, how does this probability compare to the probability of the succeeding ball being of an overcorrected line - unconditional on the preceding ball producing the same outcome? By asking the second question, we will partial out the confounding influence of the stickiness of bowling plans.
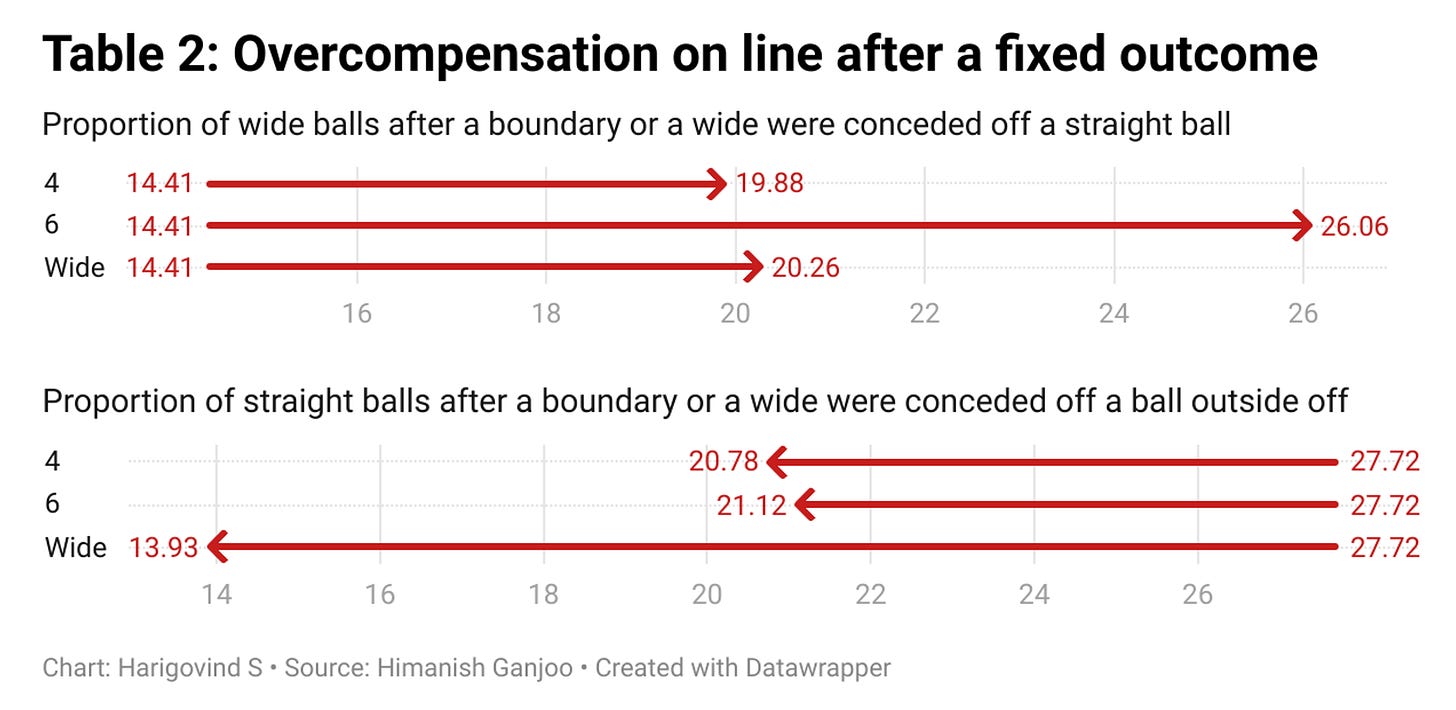
The results are listed in Table 2. Two broad conclusions can be taken. Heterogenous effects are indeed common: after conceding a four off a straight ball, bowlers overcompensate 19.88% of the time by bowling a wide one, up from 14.41% if we do not filter out preceding balls that don’t go for a boundary. A six makes this even more likely: not only does the incidence of a maximum diminish the correlation between the line of the preceding ball and the succeeding ball to statistically zero, but it also causes bowlers to send down a ball far outside offstump a quarter of the times. The effect of bowling a wide down leg is comparatively limited, but still nonnegligible. These results are statistically significant at the 1% level and are robust to using different definitions of a wide line.
A second key conclusion is that bowlers overcompensate after erring on the pads but there is no general trend of overcorrection if they drift wide. Using various definitions of the wide line, spanning from 1m away from the stumps to 0.4m, never does the proportion of straight balls following a wide one rise over 25% (the proportion of balls aimed straighter than middle stump is 27.72%). The results are similar when one compares the proportion of straight balls following a wide one being hit for a boundary with the proportion of any succeeding ball being straight. This interesting quirk is likely explained by the fact that erring wide is not as costly to bowlers as erring straight; most batters excel at hitting towards the legside but not through off.
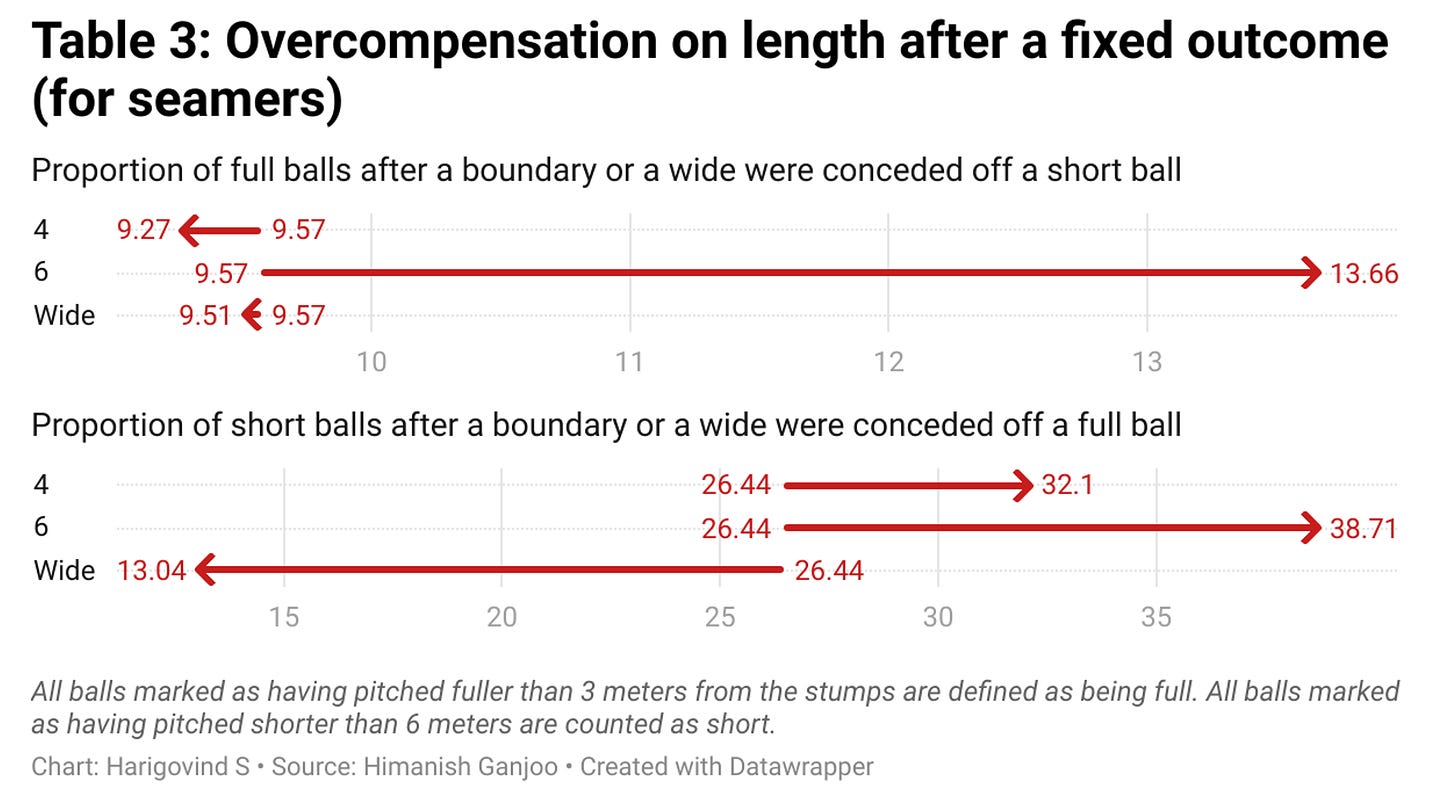
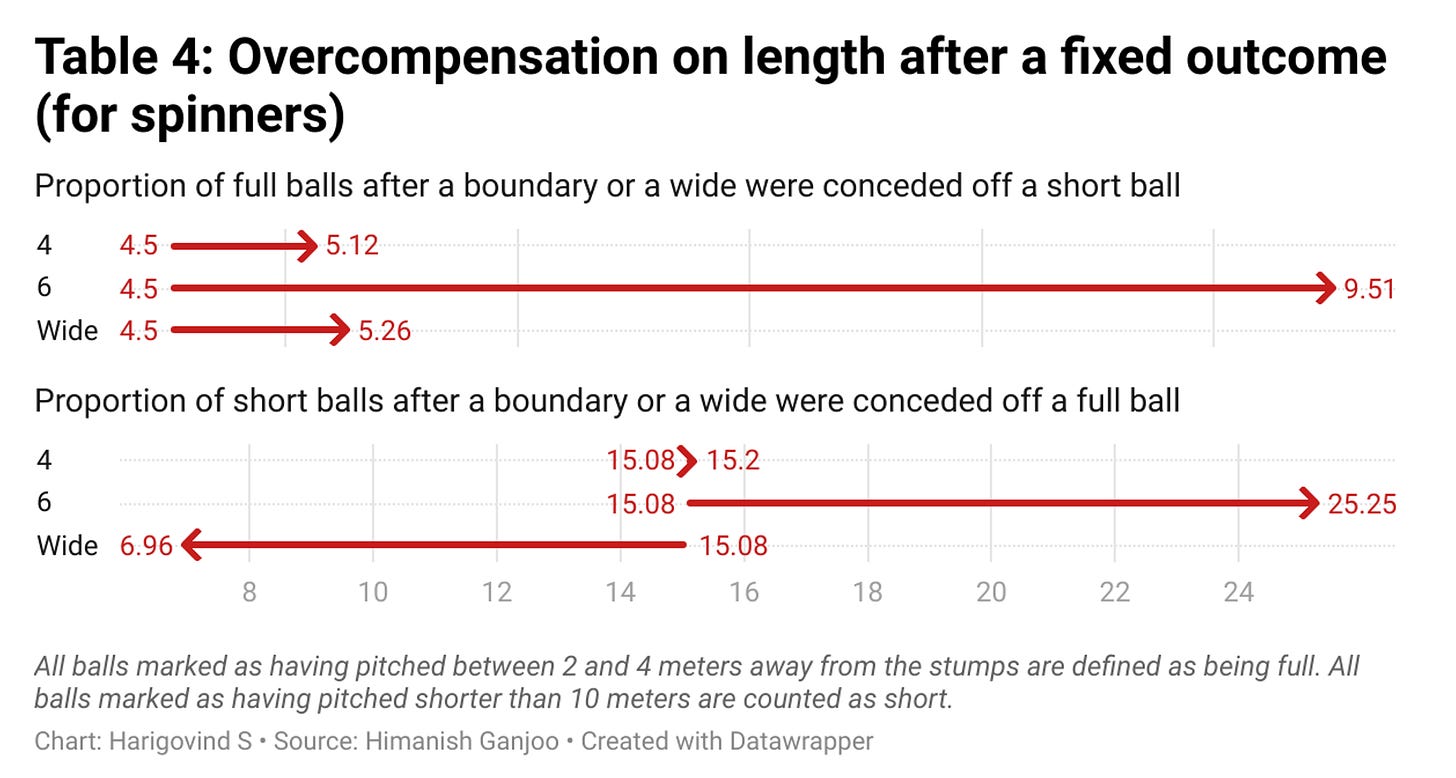
More evidence for such heterogeneity arrives from studying the overcorrection of lengths. Since spinners and seamers pitch the ball at different points to get it up to the same height, it is instructive to perform this analysis separately for each. But the results, tabulated in Tables 3 and 4, are no different from one another. In general, neither spinners nor seamers overcompensate significantly after being hit for a four - off a full or a short one - but both do after they’ve been pinged for a six. (There is a case to be made that spin bowlers may be a tad more guilty of overcompensating for a full one than are the speedsters - a third of their succeeding balls following a half-volley are short as opposed to 15% for the quicks - but this deserves more attention as such an effect could be borne out in the IPL data due to the greater incidence of domestic-quality twirlers.)
Quantifying the incidence of overcompensation at the general level is useful, but what generates actionable insight is when a batter, after he has flicked off the pads for four, is able to predict that the bowler will now overcorrect his line, and sets himself up for the cut shot. To this end, the next section of this article asks the question: which bowlers overcompensate the most, and which batters are most efficient at taking toll?
As we move towards a more specific setting, the challenge becomes retaining enough observations per player to return meaningful results. This is a classic tradeoff between bias and precision - now that we seek to understand overcompensation at the precise level of the player, the propensity for bias looms large because each bowler will have erred short and wide only a limited number of times. Consequently, this section must be taken with a pinch of salt.
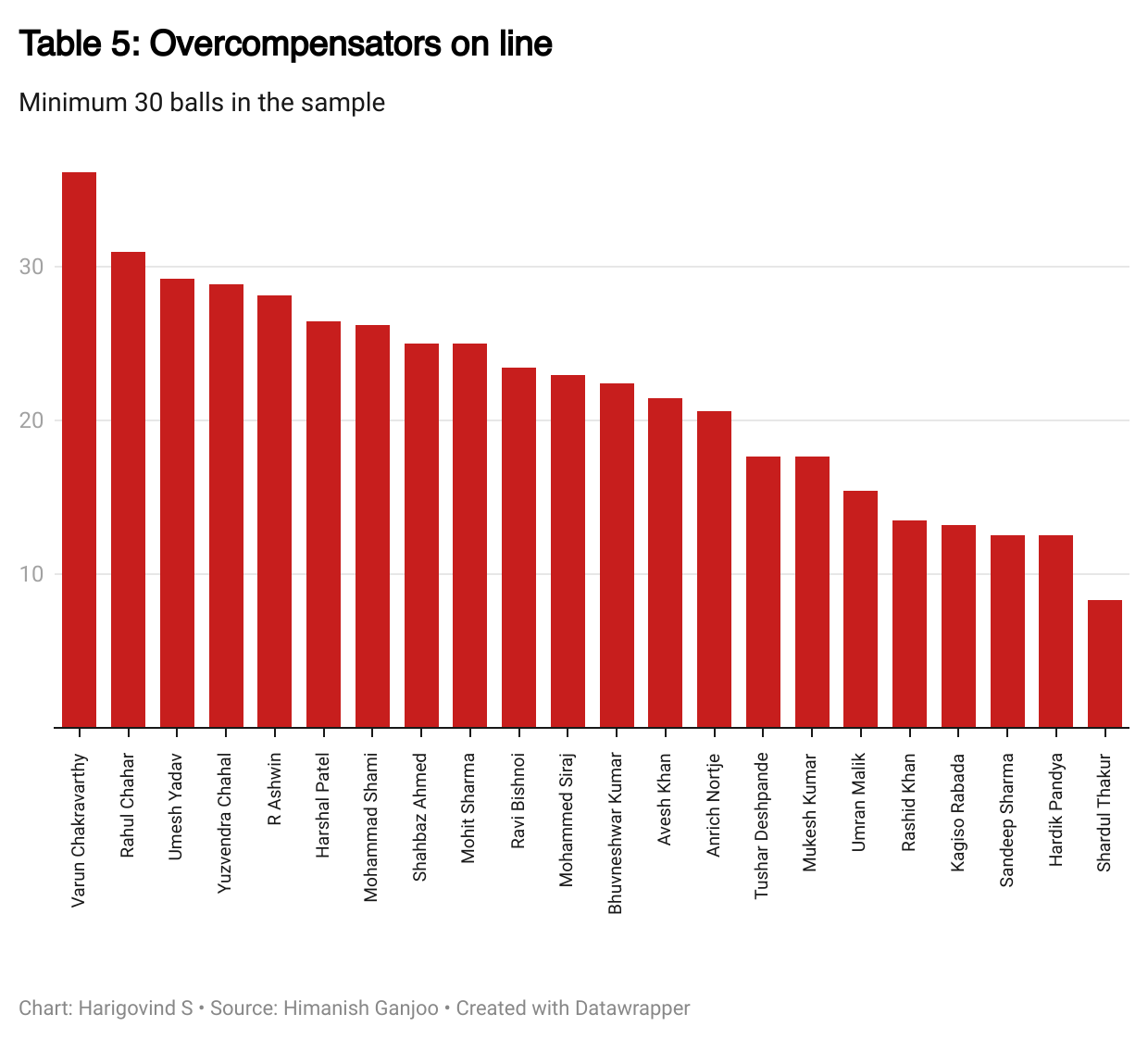
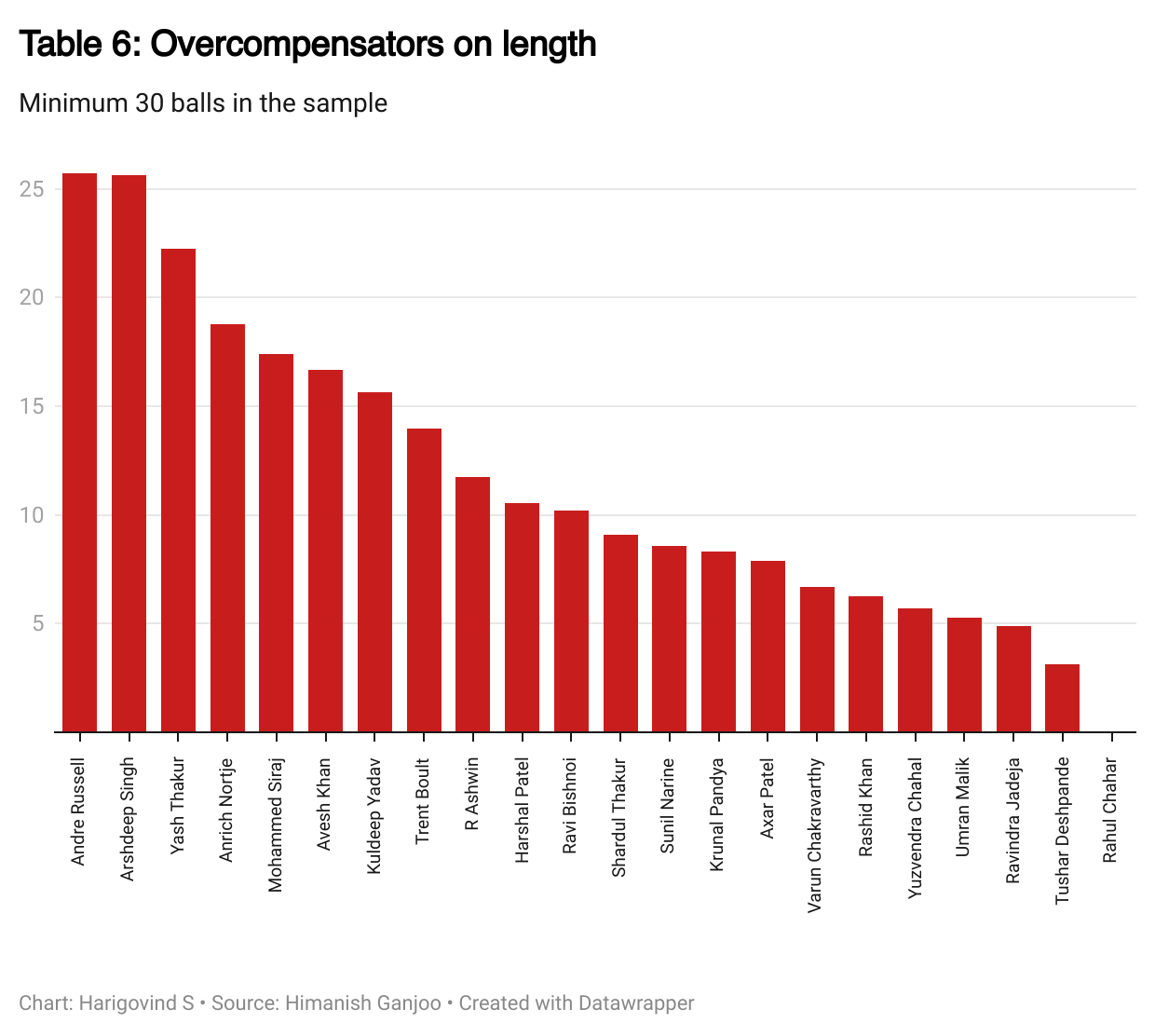
There are, however, ways of attacking this problem. One such approach is to bunch together different kinds of overcompensation. Going from wide to straight and from straight to wide can both be thought of as line overcorrection. In the same vein, going from short to full and from full to short can both be thought of as length overcorrection. This does not eliminate the sample-size issue entirely, but gives the results enough power to be considered seriously - albeit with some caution. These results can be found in Tables 5 and 6.
The careful reader will note that two types of bowlers inhabit the far edges of both tables. On the one hand are accurate customers such as Rashid Khan and Ravindra Jadeja, who stick to their guns even when they have been whacked for a boundary. Many of these players must be stubborn; others accurate. At the other end of the spectrum are those like R Ashwin, who ascribe heavy weight to the instant but insufficient evidence of a single ball being hit for a boundary and immediately change tack. It is possible that Ashwin does this out of intention, whereas somebody like Umesh Yadav does it out of unintended correction.
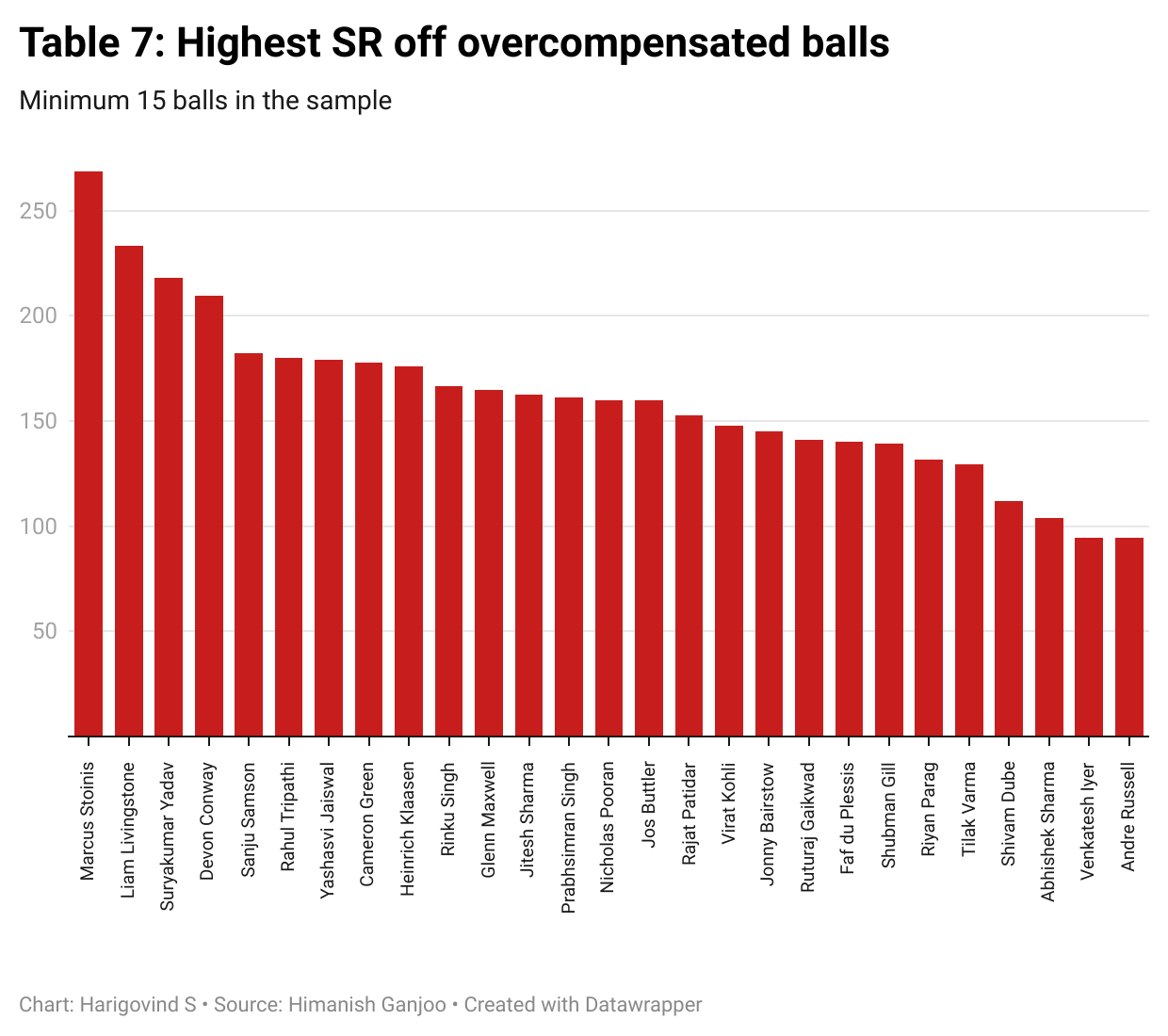
Since there are more batters than bowlers in every team, the sample size per batter is very low. Thus, we must zoom out a bit more to obtain sensible results. Table 7 plots the strike-rate of batters off any straight, wide, short or full ball where a bowler has overcompensated after the same batter has scored a four or six off them. Of batters to have faced at least 15 such deliveries in the last three IPLs, Marcus Stoinis has the highest strike-rate with 268.75. Other notable entries include Liam Livingstone, Suryakumar Yadav, Heinrich Klaasen and Maxwell. Curiously, Andre Russell lurks at the bottom, striking at under run a ball against such deliveries.
These are imprecisely estimated rankings, but they still give a few pointers to keep in mind for batters and bowlers as they face up against each other and a short or wide one gets thrown out. Above all, they show that the tendency to overcompensate not only exists, but can also be thought of as rational. Overcorrected deliveries yield a strike-rate of 137 from IPL batters, marginally down from the overall strike-rate of 142 in the last three seasons. This shows the value of variation and further speaks to the complexity of cricket, even in its most shortened version. The internal algorithm churning out cricketing outcomes is complex, so bowlers may seek to stay away from areas that they see to be hazardous - even in the very short run.
P.S. Many thanks are due to Himanish Ganjoo for selflessly sharing the data that he has taken great pains to collect and clean. The use of arrow plots in this article is inspired by his new piece for ESPNcricinfo, which reads as elegantly as a beautiful mathematical theorem. Thanks also to Stephen Nehemiah for his helpful comments on an earlier draft.




Truly good cricket stuff!
This is wonderful work! Especially the last point about overcorrection having value. You hear commentators speak a lot about overcorrection but this article really unentangles it all.